Ratio and proportion are widely used in algebra to find the division and x term. The ratio is totally relevant to fractions as all the ratios can be written in the form of p/q. on the other hand, the proportion has two ratios with an equivalent sign among them.
Ratio & proportion are used in various fields of mathematics such as algebra, geometry, triangles, etc. it is usually used to compare two terms like height, distance, mass, etc.
In this article, we’ll discuss the definition and types of ratio & proportion along with a lot of examples.

What are ratios & proportions?
Let’s discuss ratios and proportions briefly.
Ratios
In mathematics, the term used to compare two values is known as ratios. The comparison of the terms tells us how much one term there is compared to the other term. In ratios, the terms should have the same units.
It is usually denoted by the “:” sign. Ratios can be written in the form of u/v, where v is not equal to zero.
For example, to compare the male and female students in a class ratios are used. If there are forty students in a classroom, where 16 are male students and 24 are female students. Then the ratio form is male students : female students = 16 : 24.
In the form of a fraction, it can be written as 16/24. Now simplify the terms to compare the male & female students, 2 : 3 or 2/3. To compare male students to female students simply rewrite ratios with the number of females first as 3:2 or 3/2.
Proportion
In algebra, a proportion is an equation of two ratios to tell you how two ratios are equal to one another. Proportion can also be written in the form of fractions. The two possible ways to write a proportion are:
- s : t : : u : v
- s / t = u / v
Types of ratio
In algebra, there are two commonly used types of ratios.
- Part to whole ratio
- Part to part ratio
1. Part to whole ratio
If two terms or things are compared in such a way that one thing is taken from the whole, then it will be the part to whole ratio. For example, if you take a piece of bread from the whole packet, then it will be the part to whole ratio.
2. Part to part ratio
A part to part ratio is that type of ratio in which different terms or things are compared. It can give the comparison of two groups. For example, the ratio between army and police, the ratio of female students in class 8 to female students in class 9 are a few examples of this type of ratio,
Types of proportion
Proportions are of two types.
- Direct proportion
- Inverse proportion
1. Direct proportion
Direct proportion is a type of proportion in which an increase in one object causes an increase in the other object or a decrease in one object causes a decrease in another object. For example, you have two objects u & v where u is the number of workers and v is the working of the construction of the wall.
If the number of workers increases then the working speed of the wall increase, or if you hire fewer workers or decrease the worker then the work should be decreased. It is a direct proportion as both u & v increase or decrease with an increase or decrease in one quantity.
2. Inverse proportion
Inverse proportion is the other type of proportion in which an increase in one quantity causes a decrease in the other quantity or a decrease in one quantity causes a decrease in another quantity. For example, x and y are two terms, where x is the number of persons in a camp and y is the food for 40 days.
If the amount of food increases then the food for 40 days will decrease, or if the number of person decreases then the amount of food should be increased.
Examples of ratios and proportions
Following are a few examples of ratio and proportions to learn how to calculate them.
Example 1: For ratios
In a wooden box, there are 16 balloons. From these 16 balloons, 7 are pink, 5 are purple, and 4 are white. Calculate the ratio of:
- Pink balloons to purple balloons
- purple balloons to total balloons
- white balloons to pink balloons
Solution
Step 1: Write the given data of balloons.
Total balloons = 16
Pink balloons = 7
purple balloons = 5
White balloons = 4
Step 2: Find the pink balloons to purple balloons
Number of pink balloons = 7
Number of purple balloons = 6
The ratio is,
7 : 6
or
7/6
Step 3: Find the ratio of purple balloons to total balloons
Number of total balloons = 16
Number of purple balloons = 5
Difference among total balloons and purple balloons = 16 – 5 = 11
Now the ratio is,
5: 11
Or
5/ 11
Step 4: Now find the ratio of white balloons to pink balloons
Number of white balloons = 4
Number of pink balloons = 7
Ratio is,
4 : 7
Or
4/ 7
Example 2: For the proportion
15 workers are required to construct a bridge in 30 days, how many workers are required to construct the same bridge in 14 days.
Solution
Step 1: Write the given data of workers & days.
Workers required to build a bridge = 15
Days = 30
Workers required to build the same bridge in 14 days = x
Step 2: Write the workers and days in the form of proportion.
workers : days : : workers : days
15 : 30 : : x : 14
Step 3: Write the ratios in the form of fractions with an equality sign among them to calculate the value of x.
15/30 = x/14
Step 4: To find the value of x, use cross multiplication and simplify the above expression.
15/30 = x/14
1/2 = x/14
1 * 14 = x * 2
14 = 2x
2x = 14
x = 14/2
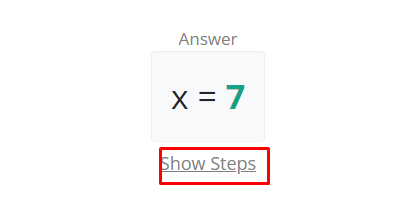
x = 7
Workers required to build the same bridge in 14 days = 15 + 7 = 22
Hence, 7 more workers are required to construct the bridge in 14 days.
You can also use a proportion calculator to find the x values of the given problems in a fraction of seconds. Follow the below steps to calculate the x value.
Step 1: Input the data values.

Step 2: Press the calculate button.

Step 3: Press the show more button to view the solution with steps.
Summary
Now you are witnessed that the ratios and proportions are not a difficult topic. You can grab all the basics of ratio & proportion just by learning the above post. Now you can solve any problem of ratios & proportions easily by following the above-mentioned examples.

Leave a Reply